原创sin(x)的快速算法(含解释)【相对误差最大0.5%】【使用移位和指针 快速计算】 未

flyerhacker

参考的算法：

点击此处下载 ourdev_598817FZ2T3S.mht(文件大小:658K) (原文件名:[译]一种简单，快速，精准的sin-cos函数模拟，及as3实现 - On the road - 博客园.mht)


#include <stdio.h>
#include <math.h>

//低精度运算 ,输入范围0到90  绝对误差最大0.05
float sin1( int x)
{
        int i=0;
        long int result = 0 , temp = 0;
       
        temp = (180 - x) * x;
        result = temp;//此处result为sin(x)结果的2^13倍
       
        for( i = 0; temp >>= 1; i++ );  //最高位位数，从 0开始
       
        //下面把result转换成float内存格式
        result = ( result << 23-i ) + ( i+113 << 23 );  //i+113=127-(13-i)-1
       
        return *( (float *) &result) ;       
}


//高精度运算 ，输入范围0到90  相对误差最大0.5%
float sin2(int x)
{
        int i=0;
        long int result = 0 , temp = 0;

        temp = ( 180 - x ) * x;
        temp = temp * ( 1619 + ( (57 * temp) >>10) );
        result=temp;//此处result为sin(x)结果的2^24倍
       
        for( i = 0; temp >>= 1; i++ );  //最高位位数，从 0开始
       
        //下面把result转换成float内存格式
        result=( result << 23-i )+ ( 102+i << 23 );//102+i=127-(24-i)-1
        return *( (float *) &result );
}



int main(void)
{
        int i = 0;
        float y1 = 0 , y2 = 0 , y = 0;

        for( i = 0; i <= 90 ; i++)
        {
                y1=sin1(i);
                 y2=sin2(i);
                y=sin(i*3.1415926/180);
                printf("i=%d sin=%.3f\tsin1=%.3f 绝对误差1=%.3f\tsin2=%.3f 相对误差2=%.3f%%\n",i,y,y1,y-y1,y2,100*(y-y2)/y);
        }

        return 0;
}

flyerhacker

i=0 sin=0.000   sin1=0.000 绝对误差1=-0.000     sin2=0.000 相对误差2=-1.#IO%
i=1 sin=0.017   sin1=0.022 绝对误差1=-0.004     sin2=0.017 相对误差2=0.475%
i=2 sin=0.035   sin1=0.043 绝对误差1=-0.009     sin2=0.035 相对误差2=0.408%
i=3 sin=0.052   sin1=0.065 绝对误差1=-0.012     sin2=0.052 相对误差2=0.338%
i=4 sin=0.070   sin1=0.086 绝对误差1=-0.016     sin2=0.070 相对误差2=0.264%
i=5 sin=0.087   sin1=0.107 绝对误差1=-0.020     sin2=0.087 相对误差2=0.247%
i=6 sin=0.105   sin1=0.127 绝对误差1=-0.023     sin2=0.104 相对误差2=0.166%
i=7 sin=0.122   sin1=0.148 绝对误差1=-0.026     sin2=0.122 相对误差2=0.141%
i=8 sin=0.139   sin1=0.168 绝对误差1=-0.029     sin2=0.139 相对误差2=0.112%
i=9 sin=0.156   sin1=0.188 绝对误差1=-0.031     sin2=0.156 相对误差2=0.079%
i=10 sin=0.174  sin1=0.208 绝对误差1=-0.034     sin2=0.174 相对误差2=0.042%
i=11 sin=0.191  sin1=0.227 绝对误差1=-0.036     sin2=0.191 相对误差2=0.001%
i=12 sin=0.208  sin1=0.246 绝对误差1=-0.038     sin2=0.208 相对误差2=-0.043%
i=13 sin=0.225  sin1=0.265 绝对误差1=-0.040     sin2=0.225 相对误差2=-0.035%
i=14 sin=0.242  sin1=0.284 绝对误差1=-0.042     sin2=0.242 相对误差2=-0.088%
i=15 sin=0.259  sin1=0.302 绝对误差1=-0.043     sin2=0.259 相对误差2=-0.088%
i=16 sin=0.276  sin1=0.320 绝对误差1=-0.045     sin2=0.276 相对误差2=-0.150%
i=17 sin=0.292  sin1=0.338 绝对误差1=-0.046     sin2=0.293 相对误差2=-0.159%
i=18 sin=0.309  sin1=0.356 绝对误差1=-0.047     sin2=0.310 相对误差2=-0.173%
i=19 sin=0.326  sin1=0.373 绝对误差1=-0.048     sin2=0.326 相对误差2=-0.191%
i=20 sin=0.342  sin1=0.391 绝对误差1=-0.049     sin2=0.343 相对误差2=-0.214%
i=21 sin=0.358  sin1=0.408 绝对误差1=-0.049     sin2=0.359 相对误差2=-0.185%
i=22 sin=0.375  sin1=0.424 绝对误差1=-0.050     sin2=0.375 相对误差2=-0.217%
i=23 sin=0.391  sin1=0.441 绝对误差1=-0.050     sin2=0.392 相对误差2=-0.254%
i=24 sin=0.407  sin1=0.457 绝对误差1=-0.050     sin2=0.408 相对误差2=-0.240%
i=25 sin=0.423  sin1=0.473 绝对误差1=-0.050     sin2=0.424 相对误差2=-0.231%
i=26 sin=0.438  sin1=0.489 绝对误差1=-0.050     sin2=0.439 相对误差2=-0.227%
i=27 sin=0.454  sin1=0.504 绝对误差1=-0.050     sin2=0.455 相对误差2=-0.228%
i=28 sin=0.469  sin1=0.520 绝对误差1=-0.050     sin2=0.471 相对误差2=-0.234%
i=29 sin=0.485  sin1=0.535 绝对误差1=-0.050     sin2=0.486 相对误差2=-0.245%
i=30 sin=0.500  sin1=0.549 绝对误差1=-0.049     sin2=0.501 相对误差2=-0.261%
i=31 sin=0.515  sin1=0.564 绝对误差1=-0.049     sin2=0.516 相对误差2=-0.282%
i=32 sin=0.530  sin1=0.578 绝对误差1=-0.048     sin2=0.531 相对误差2=-0.254%
i=33 sin=0.545  sin1=0.592 绝对误差1=-0.048     sin2=0.546 相对误差2=-0.285%
i=34 sin=0.559  sin1=0.606 绝对误差1=-0.047     sin2=0.561 相对误差2=-0.267%
i=35 sin=0.574  sin1=0.620 绝对误差1=-0.046     sin2=0.575 相对误差2=-0.255%
i=36 sin=0.588  sin1=0.633 绝对误差1=-0.045     sin2=0.589 相对误差2=-0.248%
i=37 sin=0.602  sin1=0.646 绝对误差1=-0.044     sin2=0.603 相对误差2=-0.247%
i=38 sin=0.616  sin1=0.659 绝对误差1=-0.043     sin2=0.617 相对误差2=-0.250%
i=39 sin=0.629  sin1=0.671 绝对误差1=-0.042     sin2=0.631 相对误差2=-0.259%
i=40 sin=0.643  sin1=0.684 绝对误差1=-0.041     sin2=0.644 相对误差2=-0.221%
i=41 sin=0.656  sin1=0.696 绝对误差1=-0.040     sin2=0.658 相对误差2=-0.240%
i=42 sin=0.669  sin1=0.708 绝对误差1=-0.038     sin2=0.671 相对误差2=-0.213%
i=43 sin=0.682  sin1=0.719 绝对误差1=-0.037     sin2=0.683 相对误差2=-0.191%
i=44 sin=0.695  sin1=0.730 绝对误差1=-0.036     sin2=0.696 相对误差2=-0.226%
i=45 sin=0.707  sin1=0.742 绝对误差1=-0.034     sin2=0.709 相对误差2=-0.215%
i=46 sin=0.719  sin1=0.752 绝对误差1=-0.033     sin2=0.721 相对误差2=-0.209%
i=47 sin=0.731  sin1=0.763 绝对误差1=-0.032     sin2=0.733 相对误差2=-0.158%
i=48 sin=0.743  sin1=0.773 绝对误差1=-0.030     sin2=0.744 相对误差2=-0.163%
i=49 sin=0.755  sin1=0.784 绝对误差1=-0.029     sin2=0.756 相对误差2=-0.174%
i=50 sin=0.766  sin1=0.793 绝对误差1=-0.027     sin2=0.767 相对误差2=-0.139%
i=51 sin=0.777  sin1=0.803 绝对误差1=-0.026     sin2=0.778 相对误差2=-0.161%
i=52 sin=0.788  sin1=0.813 绝对误差1=-0.024     sin2=0.789 相对误差2=-0.137%
i=53 sin=0.799  sin1=0.822 绝对误差1=-0.023     sin2=0.800 相对误差2=-0.119%
i=54 sin=0.809  sin1=0.831 绝对误差1=-0.022     sin2=0.810 相对误差2=-0.107%
i=55 sin=0.819  sin1=0.839 绝对误差1=-0.020     sin2=0.820 相对误差2=-0.100%
i=56 sin=0.829  sin1=0.848 绝对误差1=-0.019     sin2=0.830 相对误差2=-0.099%
i=57 sin=0.839  sin1=0.856 绝对误差1=-0.017     sin2=0.840 相对误差2=-0.103%
i=58 sin=0.848  sin1=0.864 绝对误差1=-0.016     sin2=0.849 相对误差2=-0.063%
i=59 sin=0.857  sin1=0.871 绝对误差1=-0.014     sin2=0.858 相对误差2=-0.079%
i=60 sin=0.866  sin1=0.879 绝对误差1=-0.013     sin2=0.866 相对误差2=-0.050%
i=61 sin=0.875  sin1=0.886 绝对误差1=-0.011     sin2=0.875 相对误差2=-0.077%
i=62 sin=0.883  sin1=0.893 绝对误差1=-0.010     sin2=0.883 相对误差2=-0.060%
i=63 sin=0.891  sin1=0.900 绝对误差1=-0.009     sin2=0.891 相对误差2=-0.048%
i=64 sin=0.899  sin1=0.906 绝对误差1=-0.007     sin2=0.899 相对误差2=-0.042%
i=65 sin=0.906  sin1=0.912 绝对误差1=-0.006     sin2=0.907 相对误差2=-0.041%
i=66 sin=0.914  sin1=0.918 绝对误差1=-0.005     sin2=0.914 相对误差2=0.002%
i=67 sin=0.921  sin1=0.924 绝对误差1=-0.004     sin2=0.921 相对误差2=-0.009%
i=68 sin=0.927  sin1=0.930 绝对误差1=-0.003     sin2=0.927 相对误差2=0.024%
i=69 sin=0.934  sin1=0.935 绝对误差1=-0.001     sin2=0.934 相对误差2=0.001%
i=70 sin=0.940  sin1=0.940 绝对误差1=-0.000     sin2=0.939 相对误差2=0.022%
i=71 sin=0.946  sin1=0.945 绝对误差1=0.001      sin2=0.945 相对误差2=0.038%
i=72 sin=0.951  sin1=0.949 绝对误差1=0.002      sin2=0.951 相对误差2=0.047%
i=73 sin=0.956  sin1=0.953 绝对误差1=0.003      sin2=0.956 相对误差2=0.051%
i=74 sin=0.961  sin1=0.958 绝对误差1=0.004      sin2=0.961 相对误差2=0.049%
i=75 sin=0.966  sin1=0.961 绝对误差1=0.005      sin2=0.966 相对误差2=0.041%
i=76 sin=0.970  sin1=0.965 绝对误差1=0.005      sin2=0.970 相对误差2=0.076%
i=77 sin=0.974  sin1=0.968 绝对误差1=0.006      sin2=0.974 相对误差2=0.057%
i=78 sin=0.978  sin1=0.971 绝对误差1=0.007      sin2=0.977 相对误差2=0.081%
i=79 sin=0.982  sin1=0.974 绝对误差1=0.008      sin2=0.981 相对误差2=0.050%
i=80 sin=0.985  sin1=0.977 绝对误差1=0.008      sin2=0.984 相对误差2=0.063%
i=81 sin=0.988  sin1=0.979 绝对误差1=0.009      sin2=0.987 相对误差2=0.069%
i=82 sin=0.990  sin1=0.981 绝对误差1=0.009      sin2=0.990 相对误差2=0.070%
i=83 sin=0.993  sin1=0.983 绝对误差1=0.010      sin2=0.992 相对误差2=0.065%
i=84 sin=0.995  sin1=0.984 绝对误差1=0.010      sin2=0.994 相对误差2=0.102%
i=85 sin=0.996  sin1=0.986 绝对误差1=0.010      sin2=0.995 相对误差2=0.085%
i=86 sin=0.998  sin1=0.987 绝对误差1=0.011      sin2=0.996 相对误差2=0.111%
i=87 sin=0.999  sin1=0.988 绝对误差1=0.011      sin2=0.998 相对误差2=0.083%
i=88 sin=0.999  sin1=0.988 绝对误差1=0.011      sin2=0.998 相对误差2=0.098%
i=89 sin=1.000  sin1=0.989 绝对误差1=0.011      sin2=0.999 相对误差2=0.106%
i=90 sin=1.000  sin1=0.989 绝对误差1=0.011      sin2=0.999 相对误差2=0.109%
请按任意键继续. . .

erxun

好东西，顶一下

ilovezeno2

这个输入的都是整数吧?也就是说就能算90个值...这样还是查表更快,精度更高,空间占用也没差多少....
当然算法很有意思....

flyerhacker

这个输入可以改改，不止90个值。 呵呵

用的哪种算法我等发一下

flyerhacker

[译]一种简单，快速，精准的sin/cos函数模拟，及as3实现
看过第一篇的文章后，大呼过瘾！原文作者的思路非常简捷，有趣，偶英语比较差，欢迎指正，废话不多说看文章

原文出处：

http://www.devmaster.net/forums/showthread.php?t=5784

http://lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/


在某些情况下我们需要一些更高效的且近似于标准值的 sin 和cos函数。

有时候我们并需要过高的精度，这时 C语言中自带的三角函数（sinf() 和 cosf() f）计算的精度超出了我们所需要的精度要求，所以其效率很低。我们真正需要的是间于精度和效率的一个折中的方案。众所周知的取近似值的方法是：泰勒级数（和著名的马克劳林级数）

代码是：

x - 1/6 x^3 + 1/120 x^5 - 1/5040 x^7 + ...


我们绘制了下图:


(原文件名:1.jpg)


绿线是标准的sin函数，红线是4项泰勒级数展开式。这个近似值的效果看起来还不错，但是如果你仔细观察后会发现


(原文件名:2.jpg)
它在pi/2之前的效果还是很好的，但是超过了pi/2后就开始快速偏离标准sin。它在pi处的值比原来的0多了0.075.用这个方法来模拟波动忽动忽停，看起来很呆板，这个效果当然不是我们想要的。

我们可以继续增加泰勒级数项的个数来减小误差，但是这将导致我们的公式非常的冗长。用4项的泰勒级数展开式需要我们进行7次乘法和3次加法来完成。泰勒级数不能同时满足我对精度和效率的要求。

刚刚近似如果能满足sin（pi）=0就好了。从上图我还可以发现另一件事：这个曲线看起来很象抛物线！所以我们来寻找一个尽可能和sin接近的抛物线（公式）。抛物线的范式方程是：A + B x + C x^2.这个公式可以让们控制三个自由度。显然我们需要其满足sine(0) = 0, sine(pi/2) = 1 and sine(pi) = 0. 这样我们就得到了3个等式。A + B 0 + C 0^2 = 0

A + B pi/2 + C (pi/2)^2 = 1

A + B pi + C pi^2 = 0

解得：A = 0, B = 4/pi, C = -4/pi^2.我们的抛物线诞生啦！


(原文件名:3.jpg)

貌似这个的误差看起来比泰勒级数还要遭。其实不是的！这种方法的最大误差是0.056.（译者：而且这种近似值没有误差积累）而且这个近似值的绘制出的波动是光滑的，而且只需要3次乘法和一次加法。不过它还不够完美。下图是[-pi, pi] 之间的图像：



(原文件名:4.jpg)

显然我们至少需要它在1个完整的周期内都符合我们要求。但是我们可以看出，我们缺少的另一半是原抛物线的一个映射。它的公式是：4/pi x + 4/pi^2 x^2。所以我们可以直接这样写：

Code:

if(x > 0) { y = 4/pi x - 4/pi^2 x^2; } else { y = 4/pi x + 4/pi^2 x^2; }

添加一个条件分支不是一个好的方法。它会让程序渐渐的变慢。但是观察一下我们模拟的和标准的图像是多么的接近啊！观察上面两式子，只是中间的一项正负号不同，我的第一个单纯的想法是可以提取x的正负号来消除分支，即使用：x / abs(x)。除法的代价是非常大的，我们来观察一下现在的公式： 4/pi x - x / abs(x) 4/pi^2 x^2。将除法化简后我们得到：4/pi x - 4/pi^2 x abs(x).所以只需要多一步运算我们就得到了我们需要的sin逼近值！下图是结果



(原文件名:5.jpg)

接下来我们要考虑cos。有基础的三角公理可以知道：cos(x) = sin(pi/2 + x).把x多加一个pi/2就可以搞定了？事实上它的某一部分不是我们期望得到的。


(原文件名:6.jpg)

我们需要做的就是当x > pi/2时“跳回”。这个可以由减去2 pi来实现。

Code:

x += pi/2;

if(x > pi) // Original x > pi/2 { x -= 2 * pi; // Wrap: cos(x) = cos(x - 2 pi)}

y = sine(x);


又出现了一个分支，我们可以用逻辑“与”来消除它，像是这样：

x -= (x > pi) & (2 * pi);

Code:

x -= (x > pi) & (2 * pi);


注意这并不是c的源代码。但是这个应该可以说明它是怎么样运行的。当x > pi是false 时，逻辑“与”（&）运算后得到的是0，也就是（x-=0）大小没有改变，哈哈完美的等价!我会给读这篇文章的读者留一些关于这个练习。虽然cos 比sin需要多一些运算，但是相比之下貌似也没有更好方法可以让程序更快了。现在我们的最大误差是0.056 ，四项泰勒级数展开式每一次都会有一点点误差。再来看看我们sin函数：


(原文件名:7.jpg)

现在是不是不能继续提升精准度了呢？当前的版本已经可以满足大多度sin函数的应用了。但是对一些要求更高一些的程序现在做的还够。

仔细观察图像，你会注意到我们的近似值总是比真实值大，当然除了0，pi/2 和 pi。所以我们要做的就是在不改变这些点（0，pi/2 和 pi）的情况下，将函数再“按下去”一些。解决方法是利用抛物线的平方。看起来就像这样：



(原文件名:8.jpg)


注意它保持着原来那些关键点，不同的是它比真实的sin函数值更低了。所以我们可以用一个加权的平均值来使两个函数更接近。


Code:

Q (4/pi x - 4/pi^2 x^2) + P (4/pi x - 4/pi^2 x^2)^2


利用Q + P = 1. 你可以灵活的控制绝对误差或相对误差。别急我来告诉你取不同的极限结果时Q，P的值。绝对误差的最佳权值是：Q = 0.775, P = 0.225 ；相对误差的最佳权值是：Q = 0.782，P = 0.218 。让我们来看一下结果的图像。



(原文件名:9.jpg)

红线呢？它几乎被绿线完全覆盖了，这足以证明我们的近似十分完美。最大误差是0.001，50倍的提升！这个公式看起来很长，但是括号里面的公式最终得到的值是相同的，也就是说括号里的只需要被计算一次。事实上在原来的基础上只是增加了额外的2次乘法和2次加法就可以得到现在的结果。


先别高兴的太早，我们还要“制造”一个负号出来。我们需要增加一个abs()运算。最终的c代码是：

Code:

float sine(float x)

{

const float B = 4/pi;

const float C = -4/(pi*pi);

float y = B * x + C * x * abs(x);

#ifdef EXTRA_PRECISION // const float Q = 0.775;

const float P = 0.225;

y = P * (y * abs(y) - y) + y;

// Q * y + P * y * abs(y)

#endif }
所以我们仅仅是需要多加5次乘法和3次加法就可以完成了。如果我们忽略abs()这个仍然是比4项泰勒级数展开式快，更精准！Cos只需要相应的变换一下x就可以了。

(译者注：后面是汇编程序，不翻译了)

part2


我选取了最小误差的情况，用as3运行后发现提升了14倍，而且仍然是非常精准。不过你必须直接使用它，不能把它放到一个函数中，因为每调用一次额外的函数调用会削减执行效率，最终你会得到一个比Math.sin() 和 Math.cos()效率更差的结果。 还有这里会用到的三角定理：

cos(x) = sin(x + pi/2)

cos(x - pi/2) = sin(x)

下载: fastTrig.as.

可以清楚到对比结果，现在你可以用这个替换Math.sin() 和 Math.cos()了


哇哦！！！几乎是相同的精准度（14倍速度提升）



//always wrap input angle to -PI..PI
if (x< -3.14159265)
    x+= 6.28318531;
else
if (x>  3.14159265)
    x-= 6.28318531;

//compute sine
if (x< 0)
    sin= 1.27323954 * x+ .405284735 * x* x;
else
    sin= 1.27323954 * x- 0.405284735 * x* x;

//compute cosine: sin(x + PI/2) = cos(x)
x+= 1.57079632;
if (x>  3.14159265)
    x-= 6.28318531;

if (x< 0)
    cos= 1.27323954 * x+ 0.405284735 * x* x
else
    cos= 1.27323954 * x- 0.405284735 * x* x;
}

High precision sine/cosine (~8x faster)

//always wrap input angle to -PI..PI
if (x< -3.14159265)
    x+= 6.28318531;
else
if (x>  3.14159265)
    x-= 6.28318531;

//compute sine
if (x< 0)
{
    sin= 1.27323954 * x+ .405284735 * x* x;

   if (sin< 0)
        sin= .225 * (sin*-sin- sin) + sin;
   else
        sin= .225 * (sin* sin- sin) + sin;
}
else
{
    sin= 1.27323954 * x- 0.405284735 * x* x;

   if (sin< 0)
        sin= .225 * (sin*-sin- sin) + sin;
   else
        sin= .225 * (sin* sin- sin) + sin;
}

//compute cosine: sin(x + PI/2) = cos(x)
x+= 1.57079632;
if (x>  3.14159265)
    x-= 6.28318531;

if (x< 0)
{
    cos= 1.27323954 * x+ 0.405284735 * x* x;

   if (cos< 0)
        cos= .225 * (cos*-cos- cos) + cos;
   else
        cos= .225 * (cos* cos- cos) + cos;
}
else
{
    cos= 1.27323954 * x- 0.405284735 * x* x;

   if (cos< 0)
        cos= .225 * (cos*-cos- cos) + cos;
   else
        cos= .225 * (cos* cos- cos) + cos;
}



Tag标签: as3,近似值,sin,cos,优化

sz_ehome

MARK

flyerhacker

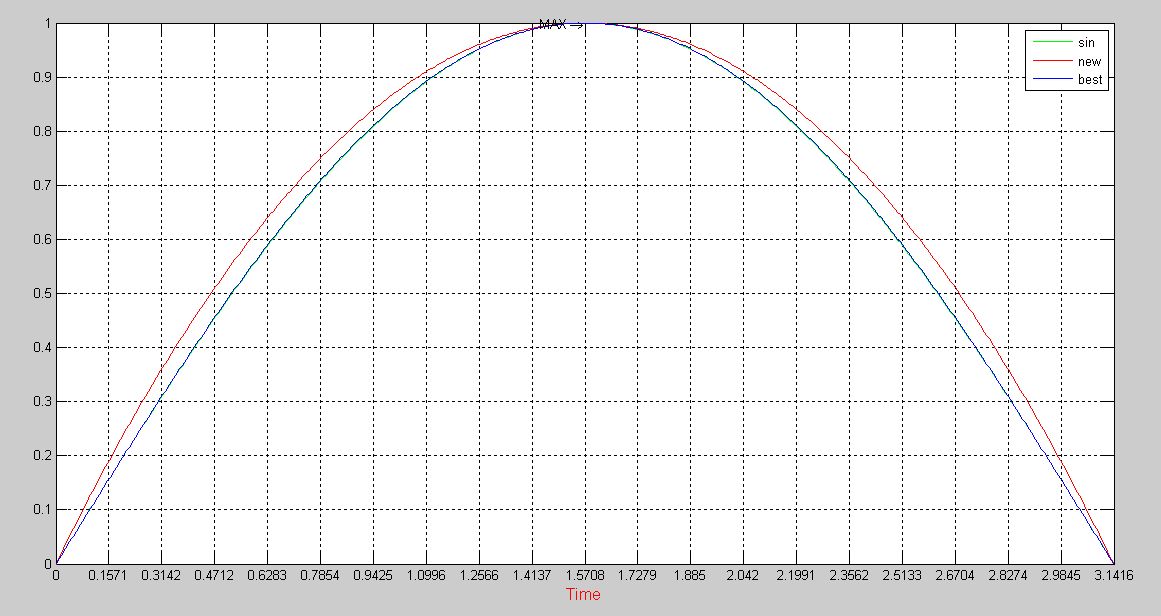
个人编写的matlab的源程序

(原文件名:截图00.jpg)





x=linspace(-pi,pi,1000);
y_sin=sin(x);
y_new=4/pi .*x - 4/pi^2.*x.*abs(x);
y_best= 0.782.*y_new + 0.218 .*(y_new.*y_new);
pic=plot(x,y_sin,'g',x,y_new,'r',x,y_best);
grid on;
axis([0 pi 0 1]);

X=-pi:pi./20:pi;
Y=0:1/10:1;
set(gca,'xtick',X,'ytick',Y) %设置网格的显示格式,gca获取当前figure的句柄


set(xlabel('Time'),'FontSize',12,'Color','r');


legend(pic,'sin','new','best')  %添加图例


[y_max,ix]=max(y_sin); %找到y1的最小值以及改值的下标，赋给y和ix
text(x(ix),y_max,'MAX \rightarrow','HorizontalAlignment','right') %插入文本

zhuyi25762

标记

XA144F

厉害，把数学应用的这么好啊！

63502925

MARK

guhenggao

mark

jielove2003

mark

ndt2000

mark

wanpujame

好东西，感谢分享

bad_fpga

好东西,MARK

liangyurongde

mark

jt6245

标记

zerttao

MAKE

linghu2

MARK

eastboy

mark 高精度快速SIN COS算法

lininglive

mark mark

yl604922959

好东西，顶一下

stoneshilin

mark

lhj200304

好像有个做游戏的公司给出了很好的sin函数，兼顾了精度和速度，有空了我对比一下看看。

lhj200304

mark  sin快速算法

linger3302

有种CORDIC算法，实际上只用到加法，随着迭代次数增加，精度提高非常快。可以算正弦余弦，正切，余切等。
甚至可以用到小波变换上。

again

CORDIC算法,我在论坛发过的哦，用过的人就知道没有其他算法比他好

flyerhacker

CORDIC算法  的确挺好的

并且精度比较高

这个只是在较快速 不需要查表的情况下使用

laolu

mark

longquan

mark

elecfun

好东西啊

cowboy

按楼主顶楼程序，用KEIL C51编译运行，测试结果并不快，sin1()为712周期，sin2()为1130周期，相比起KEIL自带的sin()函数624周期都要慢一些，而且返回值不正确，可能是由于储存格式原因，转换成float内存格式时出问题。

再测试5楼方法，sine()运行需950周期，也比自带库函数慢，且精度不算很高。

以下是测试程序：

#include <stdio.h>
#include <math.h>
#define pi 3.1415926535
#define EXTRA_PRECISION
//低精度运算 ,输入范围0到90  绝对误差最大0.05  
float sin1( int x)
{
int i=0;
long result = 0 , temp = 0;

temp = (180 - x) * x;
result = temp;//此处result为sin(x)结果的2^13倍  

for( i = 0; temp >>= 1; i++ );  //最高位位数，从 0开始  

//下面把result转换成float内存格式  
result = ( result << 23-i ) + ( i+113 << 23 );  //i+113=127-(13-i)-1

return *( (float *) &result) ;
}

//高精度运算 ，输入范围0到90  相对误差最大0.5%  
float sin2(int x)
{
int i=0;
long  result = 0 , temp = 0;

temp = ( 180 - x ) * x;
temp = temp * ( 1619 + ( (57 * temp) >>10) );
result=temp;//此处result为sin(x)结果的2^24倍  

for( i = 0; temp >>= 1; i++ );  //最高位位数，从 0开始  

//下面把result转换成float内存格式  
result=( result << 23-i )+ ( 102+i << 23 );//102+i=127-(24-i)-1
return *( (float *) &result );
}


float sine(float x)  

{

const float B = 4/pi;  

const float C = -4/(pi*pi);

float y = B * x + C * x * abs(x);

#ifdef EXTRA_PRECISION // const float Q = 0.775;  

const float P = 0.225;  

y = P * (y * abs(y) - y) + y;

// Q * y + P * y * abs(y)

#endif
return y;
}


int main(void)
{
int i = 0;
float y1 = 0 , y2 = 0 ,y3 = 0, y = 0, temp;

for( i = 0; i <= 90 ; i++)
{
  y1=sin1(i);        // 1122- 410 = 712
  y2=sin2(i);        // 2252-1122 = 1130
  temp=pi/180*i;
  y=sin(temp);       // 3211-2587 = 624
  y3=sine(temp);     // 4161-3211 = 950
  //printf("i=%d sin=%.3f\tsin1=%.3f 绝对误差1=%.3f\tsin2=%.3f 相对误差2=%.3f%%\n",i,y,y1,y-y1,y2,100*(y-y2)/y);
}

return 0;
}

dr2001

Mark一下。

result=( result << 23-i )+ ( 102+i << 23 );//102+i=127-(24-i)-1
这里的"102+i"最好加括号。包含(Resule << 23)，确认优先级。

flyerhacker

【34楼】 cowboy

高手来了 呵呵

我也没做什么测试。可能还需优化


也算是一种方法吧 呵呵

trent5145

有点意思，mark先

FlashNuk

还不错，可以借鉴。

wx85105157

回复【34楼】cowboy  
按楼主顶楼程序，用keil c51编译运行，测试结果并不快，sin1()为712周期，sin2()为1130周期，相比起keil自带的sin()函数624周期都要慢一些，而且返回值不正确，可能是由于储存格式原因，转换成float内存格式时出问题。
再测试5楼方法，sine()运行需950周期，也比自带库函数慢，且精度不算很高。
以下是测试程序：
#include &lt;stdio.h&gt;
#include &lt;math.h&gt;
#define pi 3.1415926535
#define extra_precision
//低精度运算 ,输入范围0到90  绝对误差最大0.05  
float sin1( int x)
{
int i=0;
long result = 0 , temp = 0;
temp = (180 - x) * x;
result = t......
-----------------------------------------------------------------------


内存消耗上呢？哪种消耗的多？

hetao7241

这个标记一下。

hsztc

不错

gc56198

mark

rafaa

mark!

zenith1032

mark

gaoyukun

这个必须mark~!!!

fish47

好帖马克之

yanrz

太好了，以后要好好研究下！！

winkle

mark 下周好好研究一下

avr-job

mark

zhechong

mark！

yuzr

mark

BadGuy

MARK

xyofo

学习了，谢谢

gzfslt

mark一下。好东西。

xml2028

mark

liusoldier

Mark

fw190d9

mark

xiaowei0588

很好！

yusufu

mark~

wwk1996

算法，好好看看。

fy024

不错~~~~

jacktau

谢谢分享~~~~~~~~~~~~~~~~~~~~~

bigc

mark一下

airwolf09921

今天花了1个半小时阅读了作者的原贴还有所有的跟帖，讨论的都非常专业。建议大家读一下。
从学习单片机开始就一直关注sin函数的拟合方法，这是我读到的最好的文章。
对于原文中Q和P的求取方法，麻烦哪位大侠指点一下。
作者在回帖中也提到了，把这个式子展开，貌似又回到了4级泰勒展开上面。
但是和泰勒展开不同的地方在于，作者最后的式子是在0，pi/2和pi上求未知数得到的。
而泰勒级数是由连续可导限制的。所以系数不同。
看了原文的跟帖，大家都已经讨论到了极致，SSE、汇编都出来了。很精彩。
但是我觉得，这个算法的初衷并不在于能在PC上运行多快，而是正对ARM、8位单片机这样资源有限的硬件上得到多大的效益。
不妥之处，请大家指教！